Discreteness Locus in Projective Structures

Definition:

 Let B(D,G) denote the set of hyperbolically bounded holomorphic quadratic differentials on the unit disk D for the Fuchsian group G uniformizing a once-punctured torus X. This group G is commensurable with the Fuchsian group G' uniformizing a 4-times punctured sphere Y. We may assume that Y=C-{0,1,a}, where C denotes the complex plane. Then Q:=p*(dz2/z(z-1)(z-a) ) forms a basis of the vector space B(D,G), where p:D-->Y is the canonical projection by the action of G' because B(D,G) is one-dimensional and coincides with B(D,G').
 For a complex number t, we can construct the developing map Ft from the unit disk to the Riemann sphere so that

Ft(0)=0, Ft'(0)=1, Ft''(0)=0 and
{Ft, z}= tQ(z),
where {F,z} denotes the Schwarzian derivative of F, namely, (F''/F')'-(F''/F')2/2.
Furthermore, there exists a unique homomorphism rt: G --> PSL(2,C) such thatFtog=rt(g)oFtholds for each element g in G. This is called the monodromy homomorphism or holonomy homomorphism associated with tQ(z).
Set
T(G)={t; Ft is univalent in D and admits a quasiconformal extension to the Riemann sphere}, and
K(G)={t; rt(G) is discrete in PSL(2,C)}.
T(G) is called the Bers embedding of the Teichmueller space of G and known to be equal to the connected component of Int K(G) which contains the origin (due to H. Shiga). We (Yohei Komori, Toshiyuki Sugawa, Masaaki Wada and Yasushi Yamashita) found a way to visualize these spaces. Here are some pictures drawn by Y. Yamashita. The colors in these pictures are according to the combinatorial nature of the Ford region of the corresponding monodromy image rt(G).

Example (Square Torus)

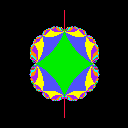
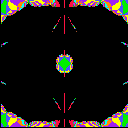
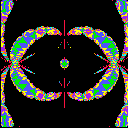
In the case below, X is the square torus with one point removed, in other words, the completion of X is the quotient space of the complex plane by the lattice group generated by 1 and i. We display the range {t=u+iv; |u|< A and |v|< A} for each picture. We can see the Bers embedding of Teichmueller space as a component of colored regions at the center of pictures.
 
A=.5 A=1 A=2 A=4
A=8 A=16 A=32

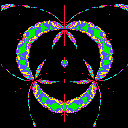
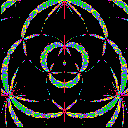
Example 2 (Equilateral Triangle)

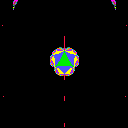
In the case below, X has the symmetry under the rotation of order 3, in other words, the completion of X is the quotient space of the complex plane by the lattice group generated by 1 and the cubic root of -1. We display the range {t=u+iv; |u|< A and |v|< A} for each picture.
 
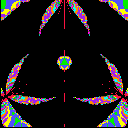A=.5 A=1 A=2
A=4 A=8 A=16

For any question or comment, please contact us

Related links:
McMullen's Gallery (many beautiful pictures)
Yamashita's Home Page (more pictures)
Wada's OPTi (cool program)
Bers Slice Project (in Japanese)
Bers Slice Project (part 2)  (in Japanese)

Back